SCNU - Side Cut Non-Uniform residual stress measurement method




Feedback and support
With any questions, bug reports, feedback and any other comments
please submit a
ticket.
Releases
24-JAN-2016: SCNURS 1.0, initial public release.
Publications and documentation
-
2016:
H.K. Kim, M.J. Pavier, A. Shterenlikht,
Measurement of Highly Non-uniform Residual
Stress Fields in Thin Plate Using a New Side Cut Destructive Method,
Proc. Residual Stresses 2016 – ICRS-10,
Eds. Thomas M. Holden, Ondrej Muransky, Lyndon Edwards,
Materials Research Proceedings 2(2016):115-120
DOI:
10.21741/9781945291173-20
-
2016:
A. Shterenlikht, H. K. Kim, Forward and inverse solutions for 2D semi-infinite strip
with self-equilibrated end loading,
README,
the most detailed explanation of the method and the code, work in progress.
-
2016:
A. Shterenlikht, Finding roots of sinx+x=0 and sinx-x=0,
short note,
PDF
-
2016:
H.K. Kim, A. Shterenlikht, M.J. Pavier, A. Velichko, N.A. Alexander,
On stability of a new side cut destructive method for
measuring non-uniform residual stress in thin plates,
Int. J Solids Struct, 100-101(2016):223-233,
DOI:
10.1016/j.ijsolstr.2016.08.019
-
2015:
H. K. Kim, BSSM Young stress analysis competition
talk.
-
2015:
H. K. Kim, M. J. Pavier, A. Shterenlikht,
Highly non-uniform residual stress measurement with reduced plastic error,
Mech Eng Dept, The University of Bristol, UK,
poster.
-
2015:
H. K. Kim, H. E. Coules, M. J. Pavier, A. Shterenlikht,
Measurement of Highly Non-Uniform Residual Stress Fields with Reduced Plastic Error,
Exp. Mech. 55(7):1211-1224,
DOI:
10.1007/s11340-015-0025-1,
PDF.
-
2014:
H. K. Kim, M. J. Pavier, A. Shterenlikht,
Plasticity and stress heterogeneity influence on
mechanical stress relaxation residual stress measurements,
Proc. of 9th European Conference
on Residual Stresses (ECRS), Troyes, France, 7-10 July 2014,
Advanced Materials Research, 996:249-255, 2014,
DOI:
10.4028/www.scientific.net/AMR.996.249,
paper
and
talk.
-
2013:
H. K. Kim, M. J. Pavier, A. Shterenlikht,
Measuring locally non-uniform in-plane residual stress with straight cuts and DIC,
Proc. 9th Int. Conf. Advances in Exp. Mechanics,
3-5 September 2013, Cardiff, Wales, UK,
The British Society for Strain Measurements (BSSM),
paper
and
talk.
-
2000:
I. A. Razumovskii, A. L. Shterenlikht,
Determining the locally-nonuniform residual-stress
fields in plane parts by the sectioning method,
J. Machinery Manufacture 4:40-45,
translated from Russian,
Allerton Press, USA, ISSN: 1052-6188.
The elastic problem
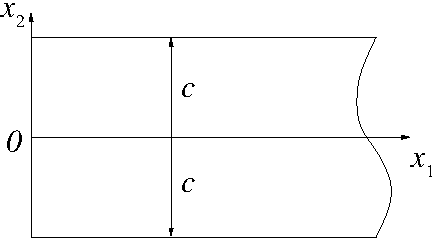
A 2D problem is assumed (x1, x2).
Residual stress is assumed to be constant through thickness,
x3.
The plate length is assumed to be much greater then width.
The method is as follows:
-
Cut on x1=0 plane.
Note that cut can be progressed along x2 or along x3, with
different effects on plastic flow.
-
Measure relaxation disp. fields, u1 and u2, e.g. with DIC.
-
Use Mathieu series 2D elastic solution to the measured displacements.
See above our papers on the analysis of plastic flow on the
measured RS fields.
Roots of the BC constraint equations
Enforcing the BC gives these 2 equations:
Each equation has an infinite number of complex roots,
which can be plotted on the complex plane:
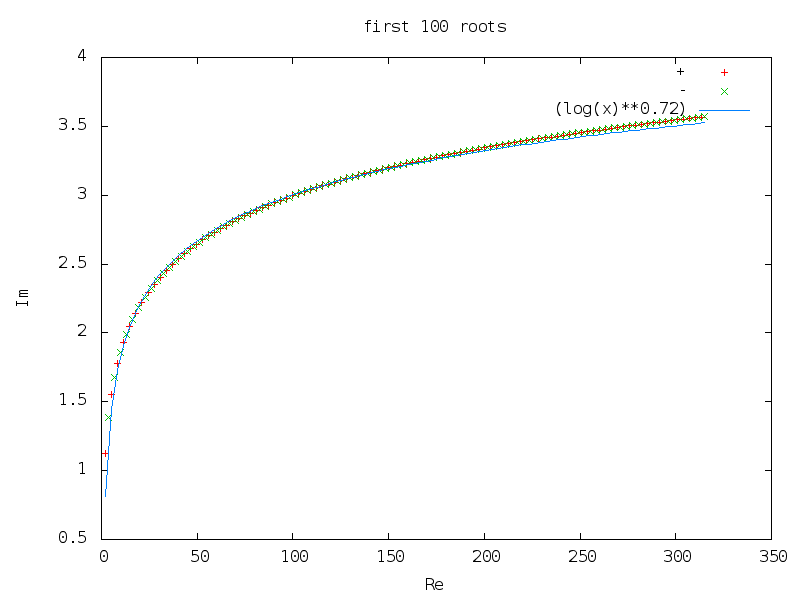
Simulated results with no error
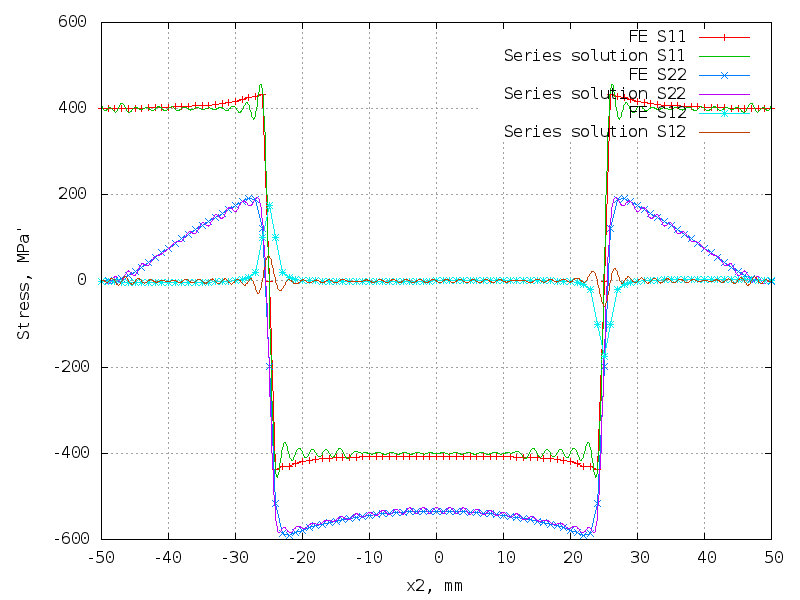
Self-equlibrated loading is applied on the end.
The forward problem is solved either analytically, or with FE.
The result is u1 and u2 disp. fields.
Then the inverse problem is solved and the series coefficients
are calculated from the displacements using LLS or rank-deficient
minimum norm LLS.
We use
Lapack.
In all plots the applied stress fields are shown with symbols.
The reconstructed fields are shown with lines.
Symmetric step res. stress field with 2 discontinuities
Anti-symm. step res. stress field with 3 discontinuities
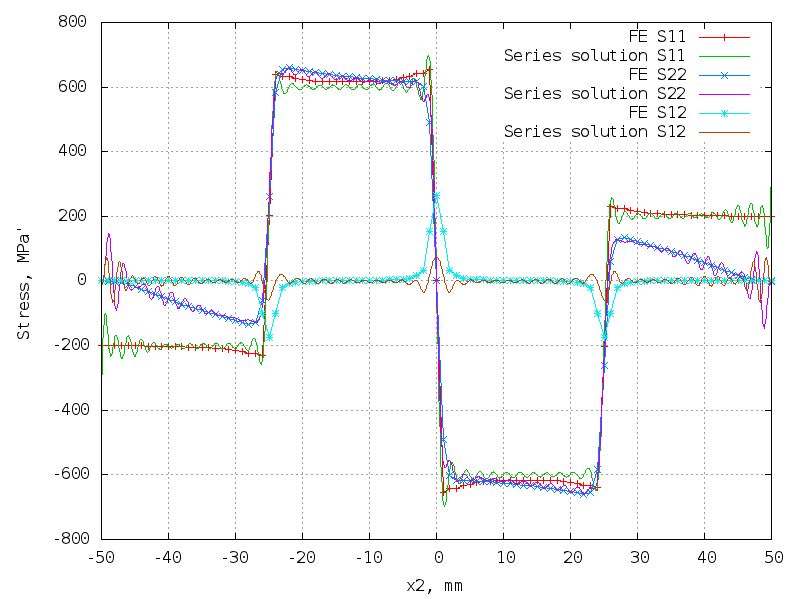
Generic step res. stress field with 3 discontinuities
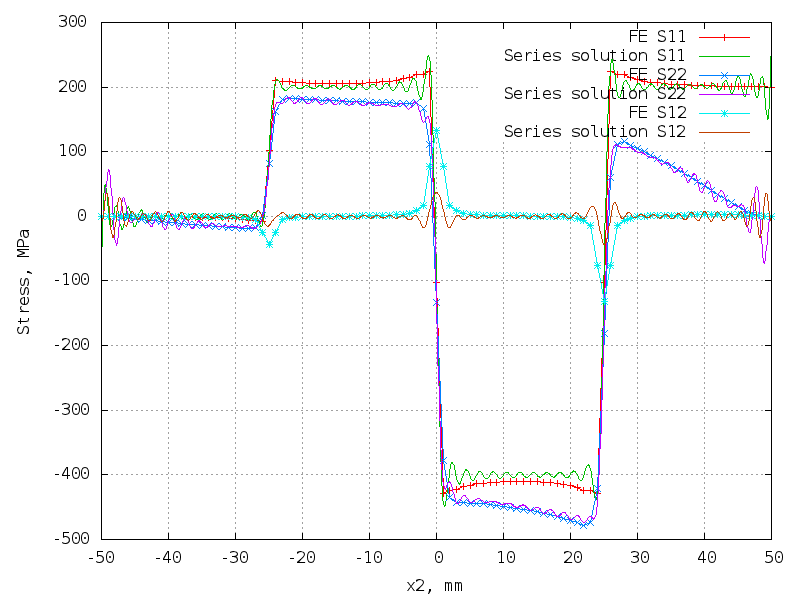
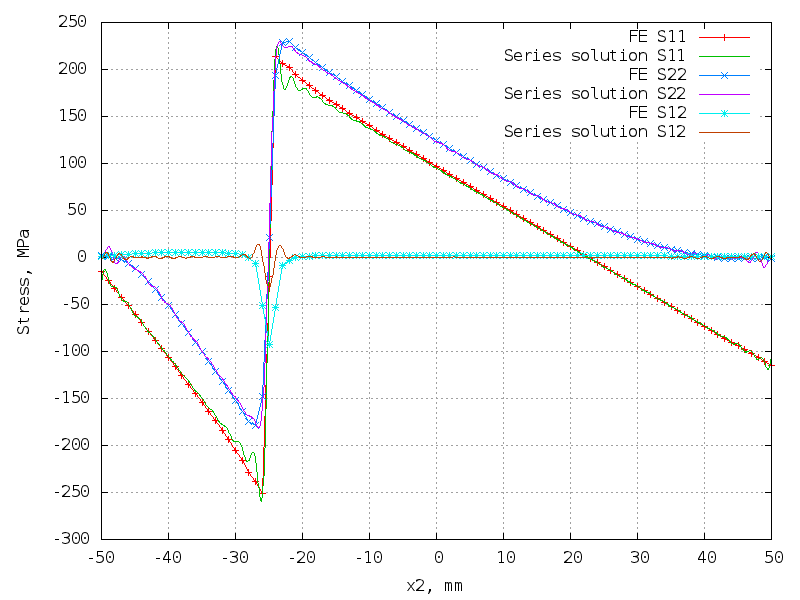
Slant res. stress field with 1 discontinuity
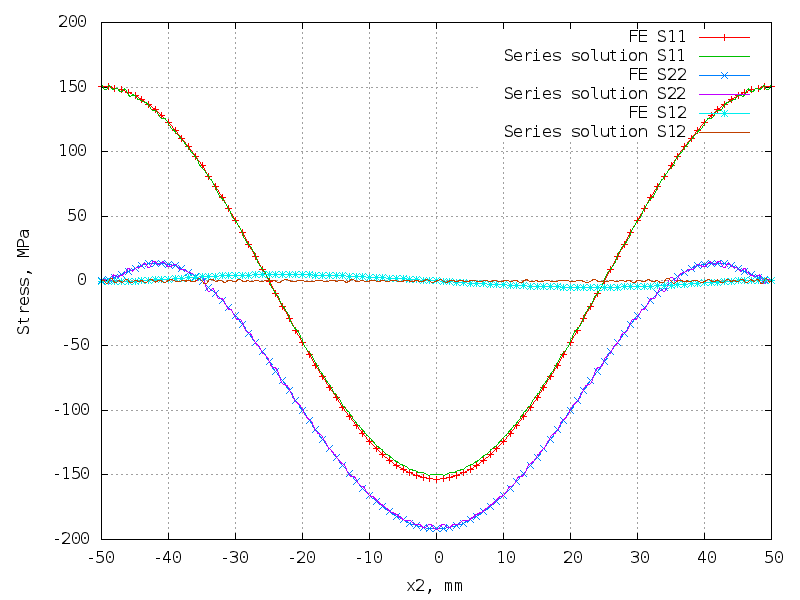
Smooth symmetric res. stress field - no discontinuities
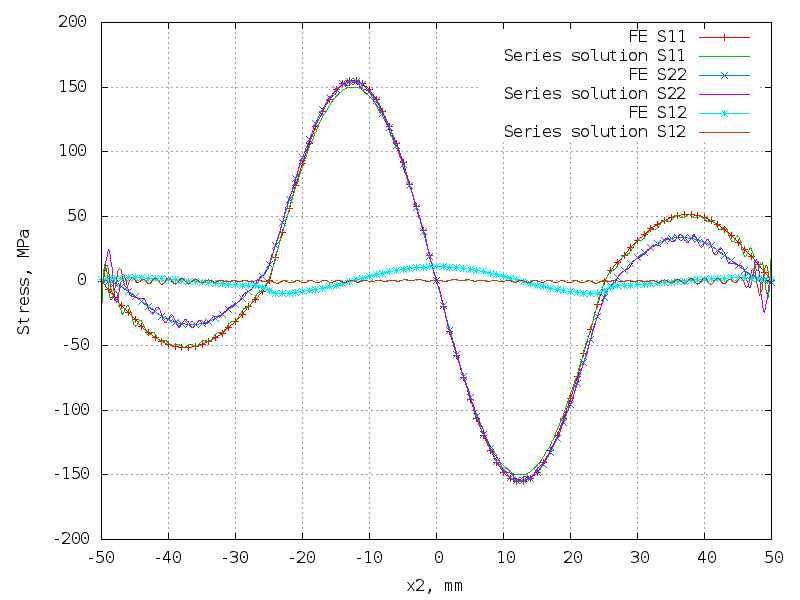
Smooth anti-symmetric res. stress field - no discontinuities
Examples of instability
The inverse problem is ill-posed i.e. ill-conditioned.
These are various manifestations.
5151 data points, 2 displacement values for each point,
so 5151*2 = 10302 equations in total.
Symmetric loading
10 terms (40 unknowns) - too coarse!
The matrix is 10302 x 40.
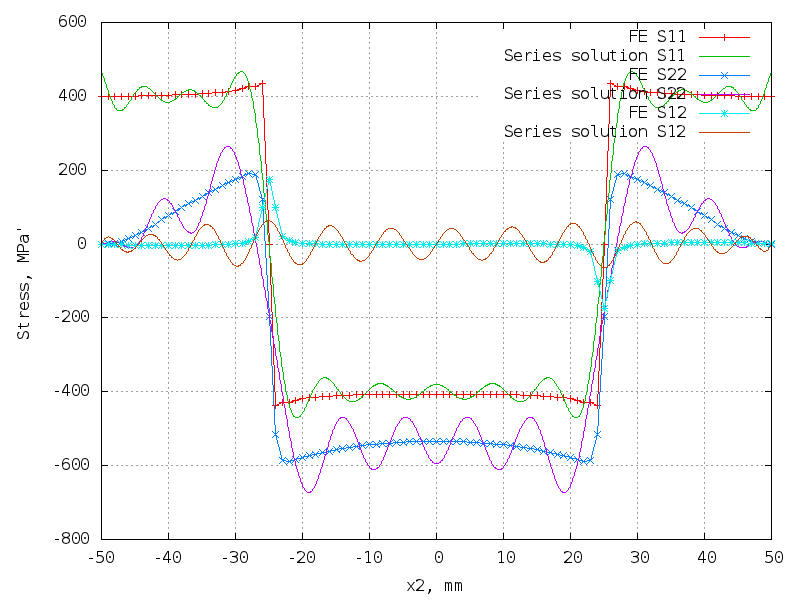
50 terms (200 unknowns) - just right!
The matrix is 10302 x 200.

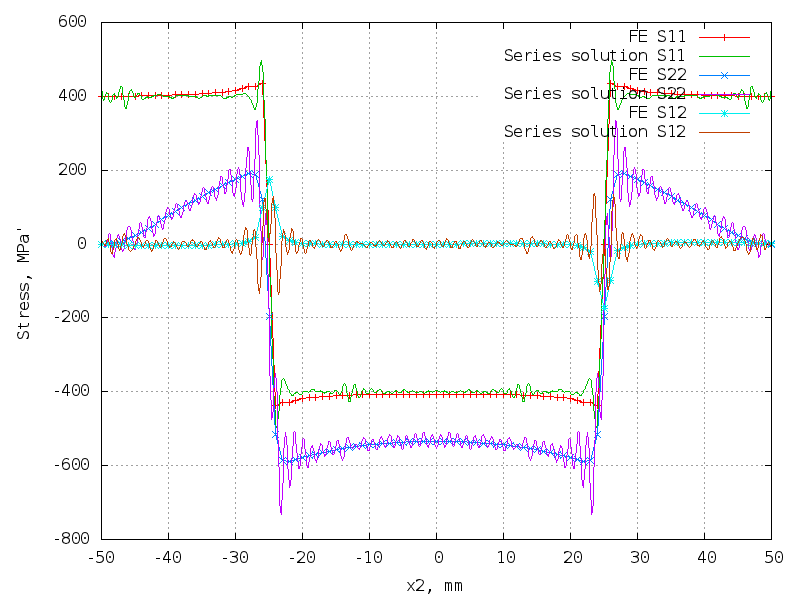
80 terms (320 unknowns) - getting worse!
The matrix is 10302 x 320.
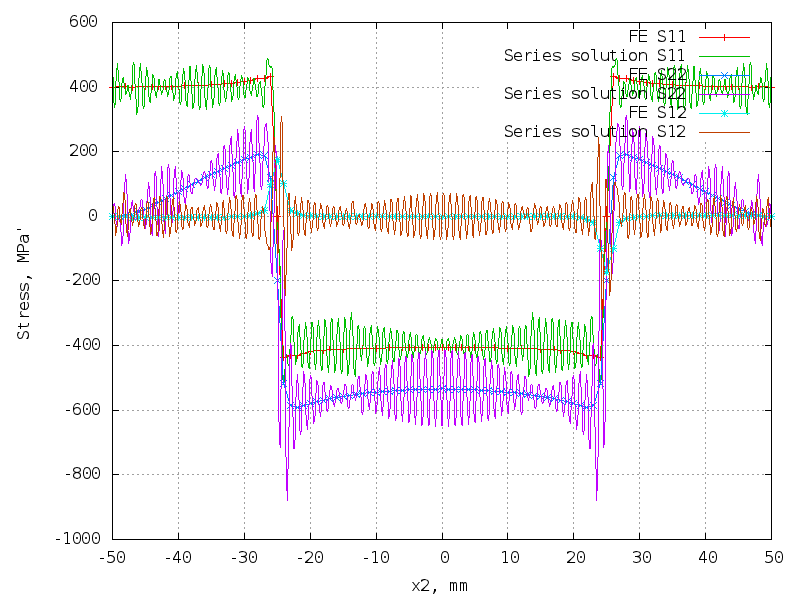
100 terms (400 unknowns) - too oscillatory!
The matrix is 10302 x 400.
Anti-symmetric loading
10 terms (40 unknowns) - too coarse!
The matrix is 10302 x 40.

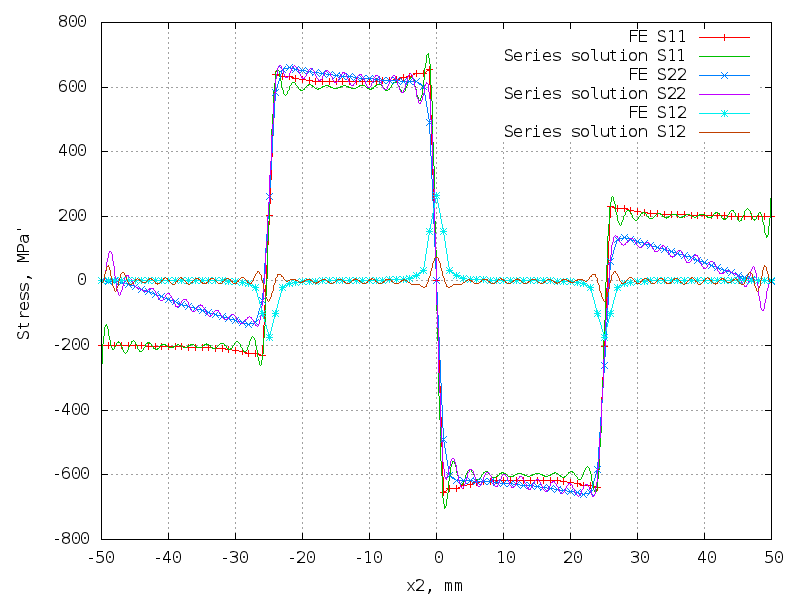
40 terms (160 unknowns) - better!
The matrix is 10302 x 160.
49 terms (196 unknowns) - best!
The matrix is 10302 x 196.

50 terms (200 unknowns) - bad!
The matrix is 10302 x 200.
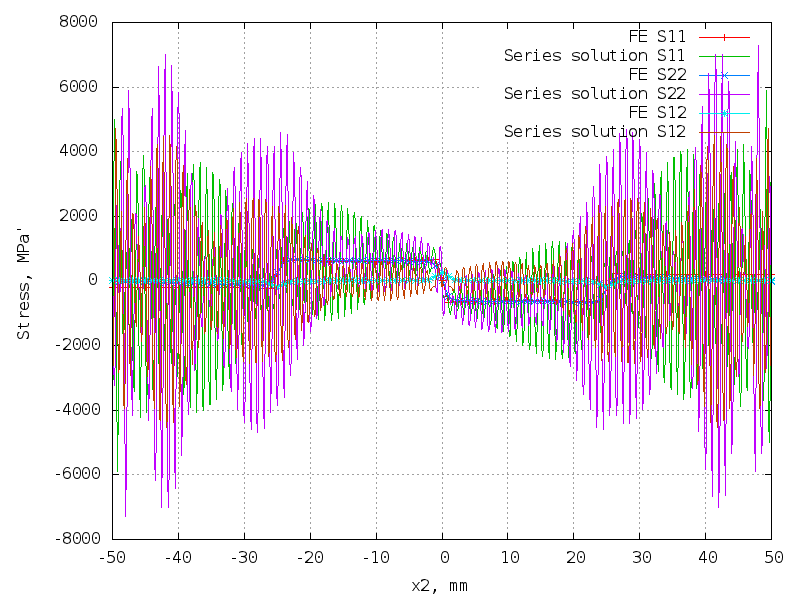
100 terms (400 unknowns) - hopeless!
The matrix is 10302 x 400.
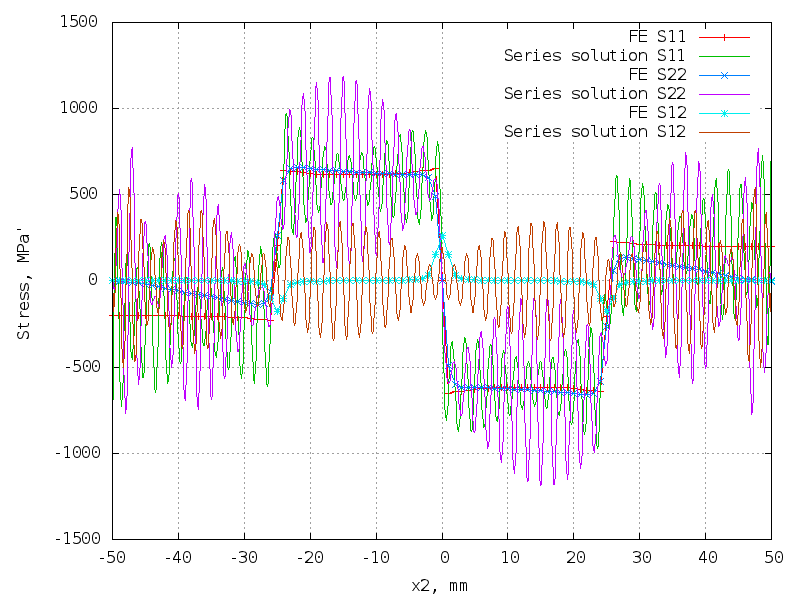
Mixed loading
10 terms (40 unknowns) - too coarse!
The matrix is 10302 x 40.
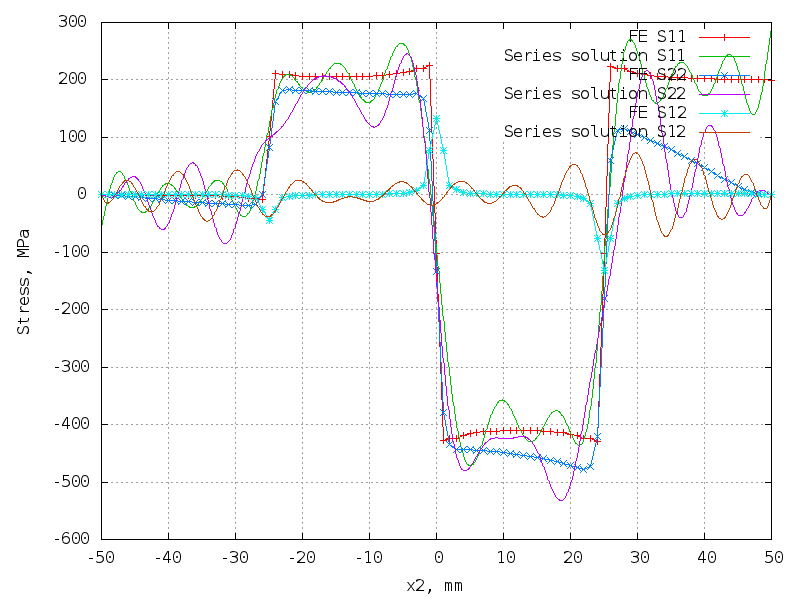
40 terms (160 unknowns) - better!
The matrix is 10302 x 160.
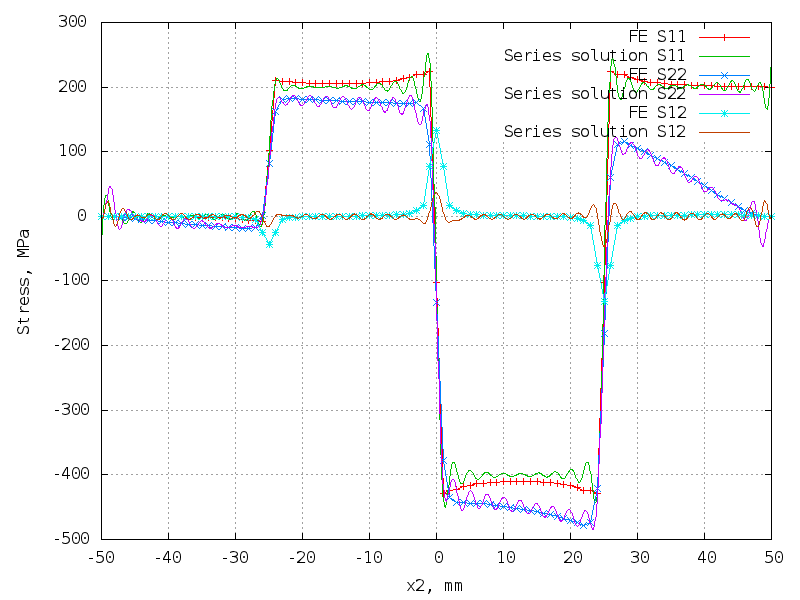
49 terms (196 unknowns) - best!
The matrix is 10302 x 196.

50 terms (200 unknowns) - bad!
The matrix is 10302 x 200.
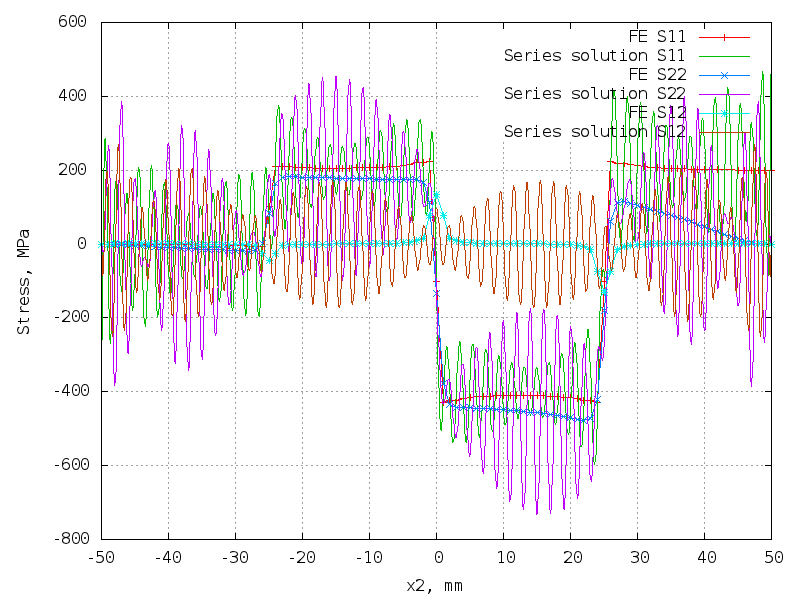
80 terms (320 unknowns) - hopeless!
The matrix is 10302 x 320.
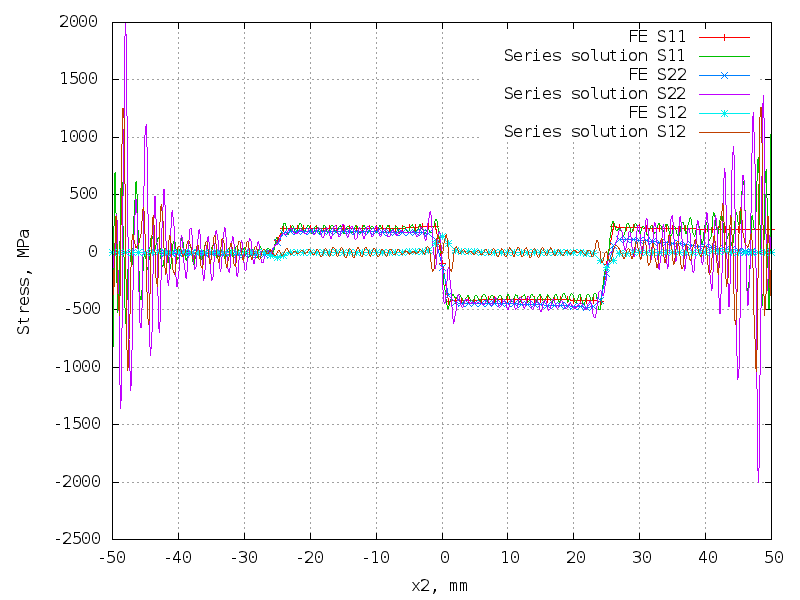
Slant loading
10 terms (40 unknowns) - too coarse!
The matrix is 10302 x 40.
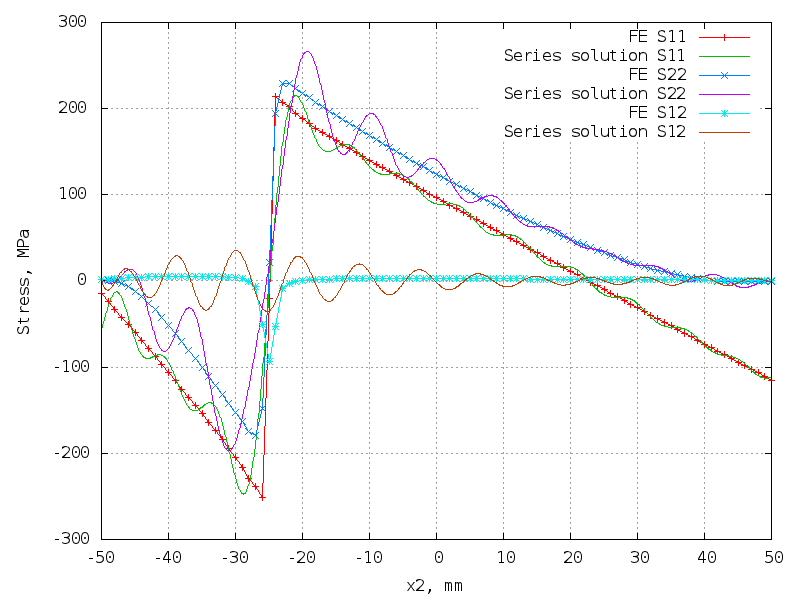
40 terms (160 unknowns) - better!
The matrix is 10302 x 160.
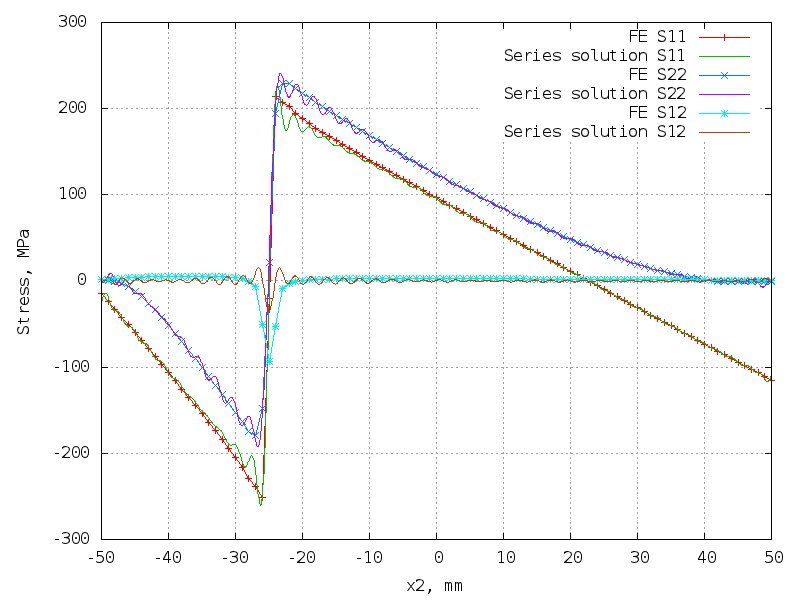
49 terms (196 unknowns) - best!
The matrix is 10302 x 196.

50 terms (200 unknowns) - bad!
The matrix is 10302 x 200.
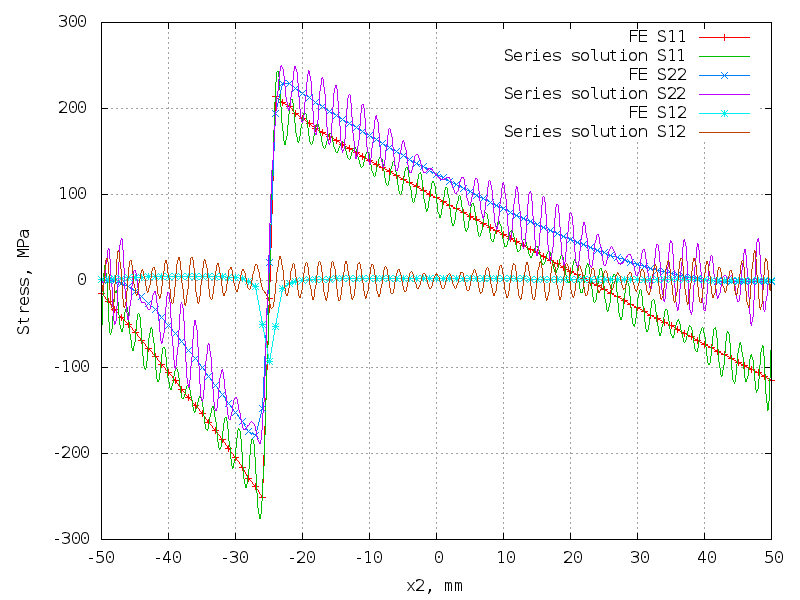
80 terms (320 unknowns) - hopeless!
The matrix is 10302 x 320.
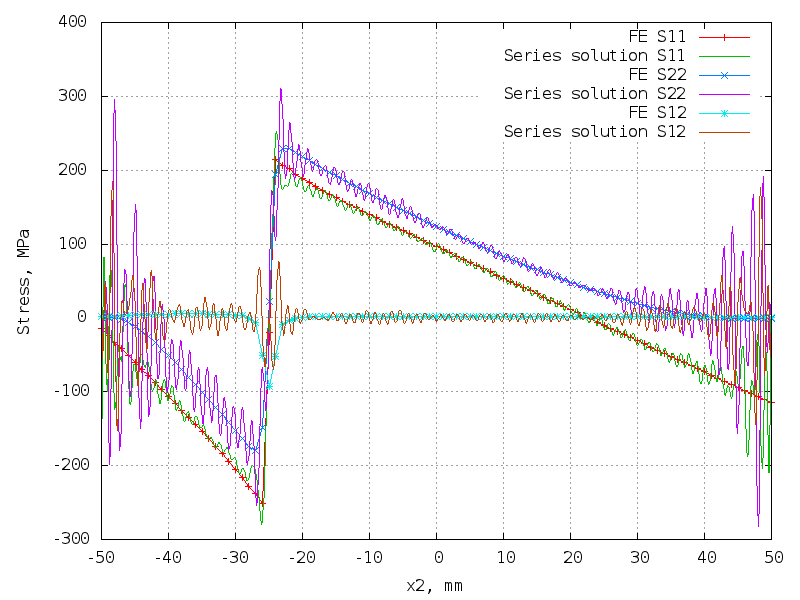
100 terms (400 unknowns) - actually beautiful!
The matrix is 10302 x 400.
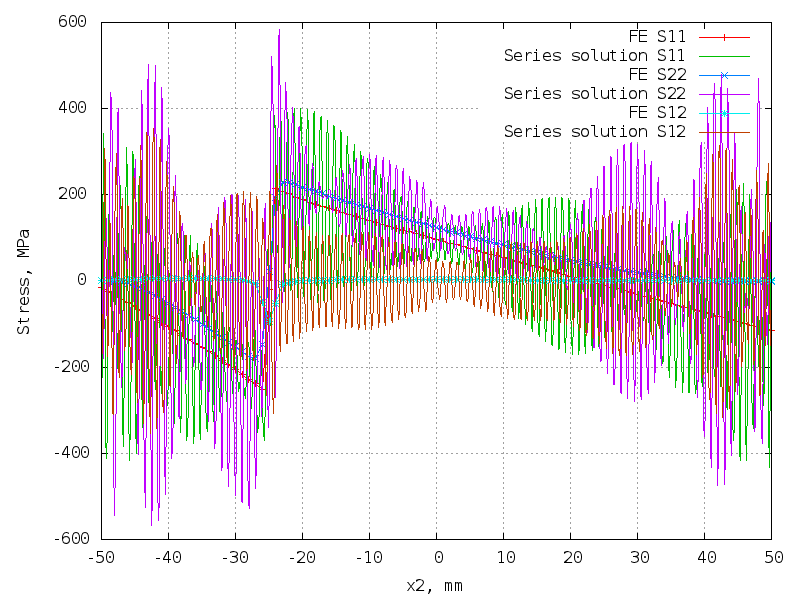
Smooth symmetric loading
5 terms (20 unknowns) - good!
The matrix is 10302 x 20.
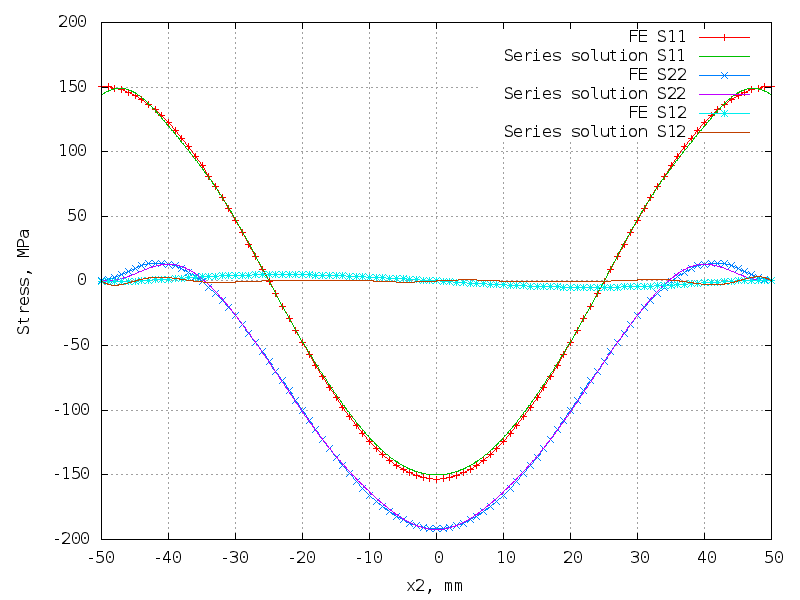
80 terms (320 unknowns) - very good!
The matrix is 10302 x 320.

100 terms (400 unknowns) - getting worse!
The matrix is 10302 x 400.
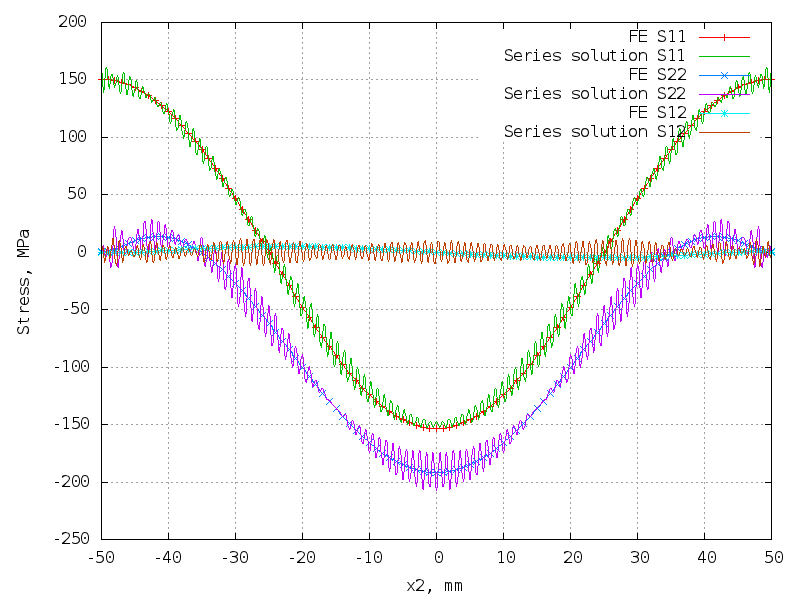
Smooth anti-symmetric loading
10 terms (40 unknowns) - good!
The matrix is 10302 x 40.
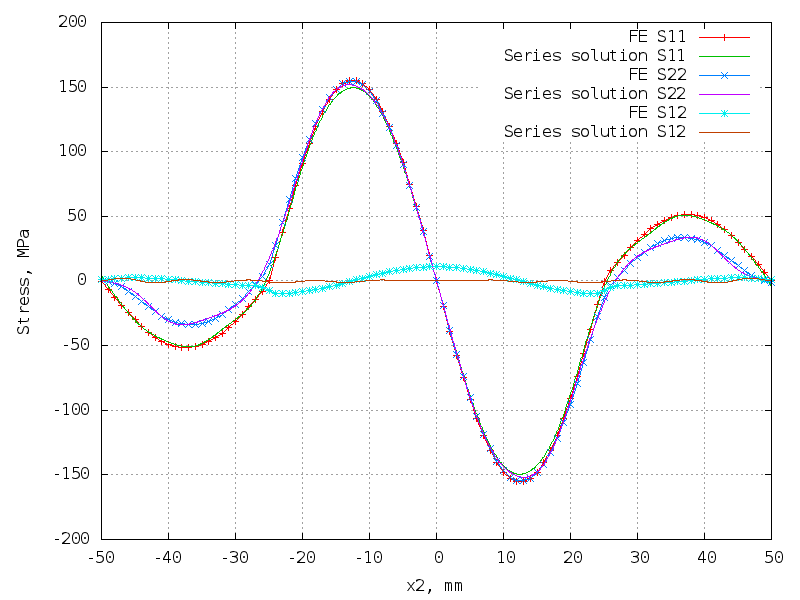
40 terms (160 unknowns) - still good!
The matrix is 10302 x 160.
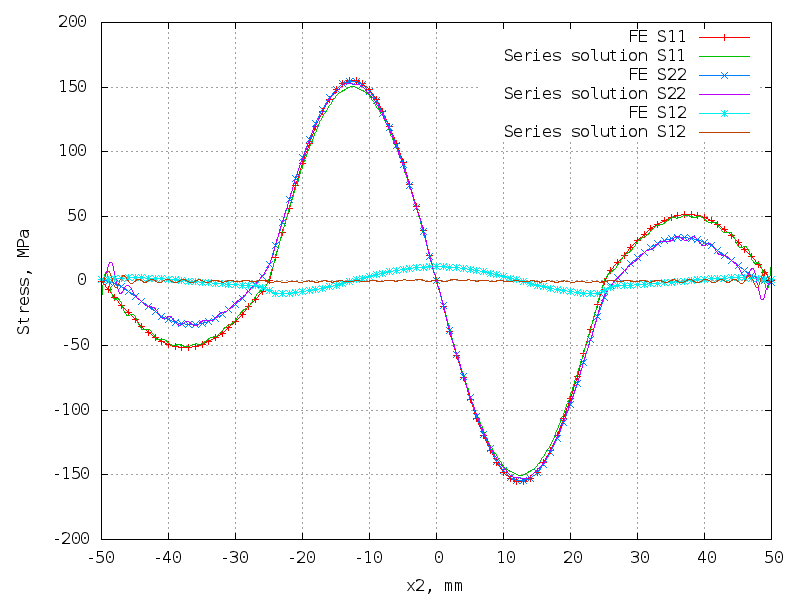
49 terms (196 unknowns) - still fine!
The matrix is 10302 x 196.

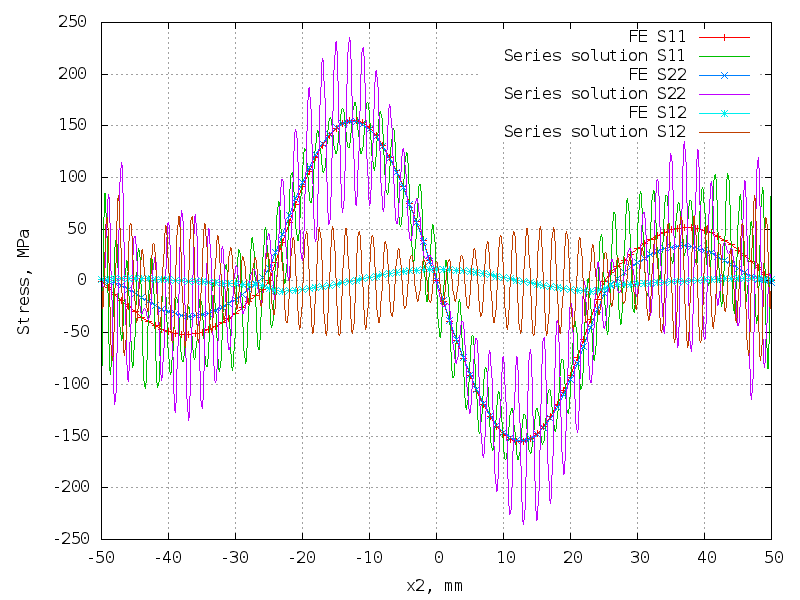
50 terms (200 unknowns) - bad!
The matrix is 10302 x 200.
Other Fortran related projects
-
ABUMPACK -
Abaqus UMAT and VUMAT for GTN, Rousselier, von Mises plasticity
-
CASUP -
Cellular Automata library for HPC and supercomputers
-
Coarrays -
Fortran 2008, 2018 coarrays course - native Fortran SPMD
parallel programming
-
CMPLX -
Validation of Fortran 2008
complex intrinsics and minus zero on branch cuts
-
OPTPACK -
OPTimisation PACKage - multi-start global
optimisation in Fortran 2003 driven with shell scripts
-
SCNU -
Side Cut Non-Uniform residual stress measurement method
-
disp2sif -
Calculation of
mixed mode (I+II) stress intensity factors (SIF)
from crack tip displacements
-
erf -
Error functions of complex arguments, erf(z), implemented in modern Fortran
validate
this page




































